Relaxation algorithms for matrix completion, with applications to seismic travel-time data interpolation

This was a project that we developed while working with Kenneth Creager, Carl Ulberg, and Rajiv Kumar. It was accepted by Inverse problems and can be found here.

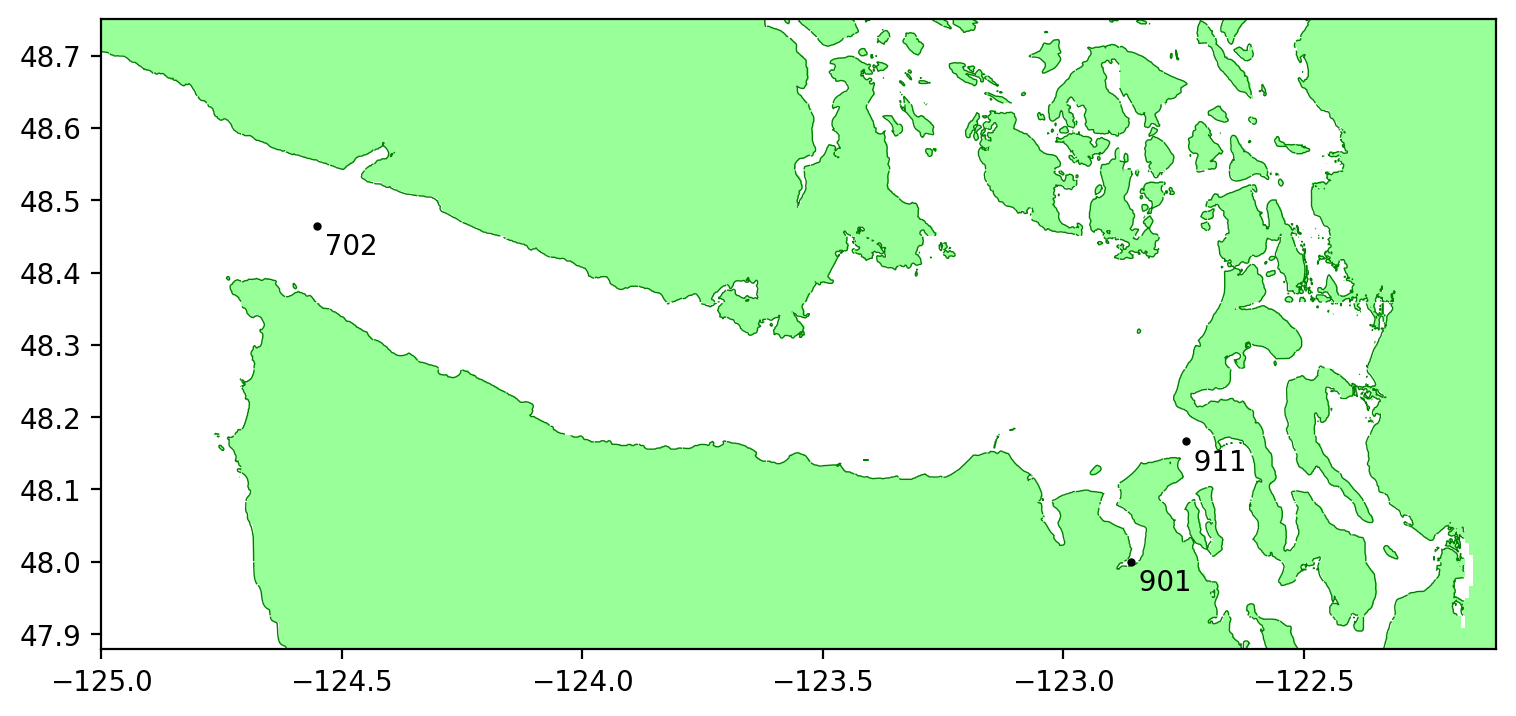
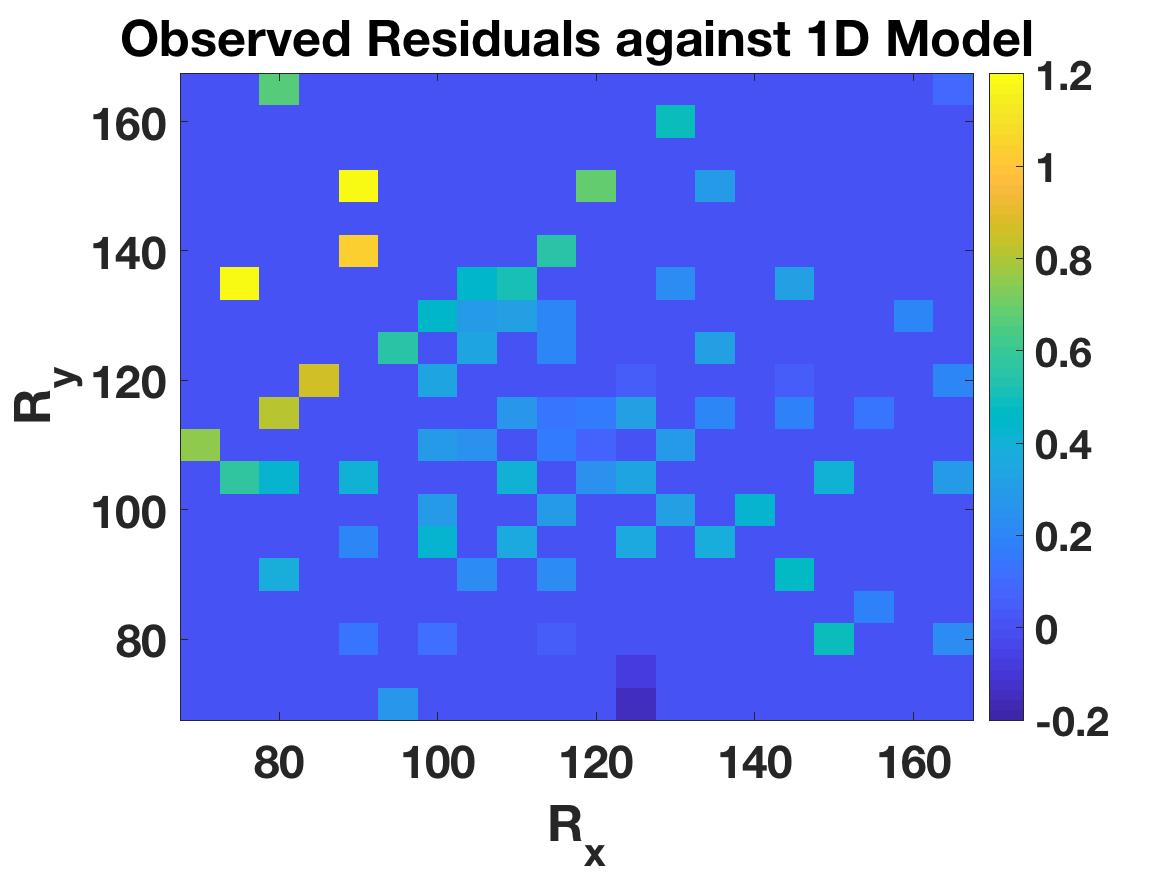
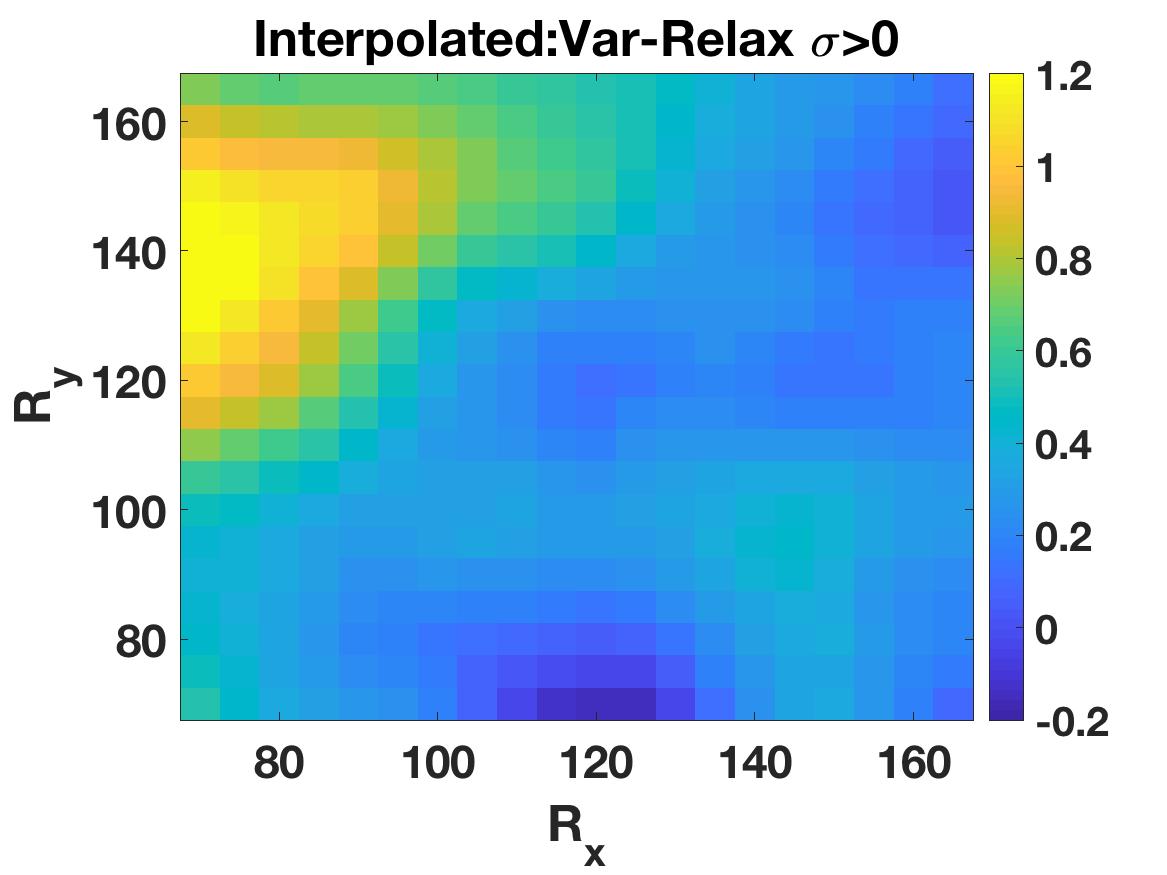
Travel time tomography is used to infer the underlying three-dimensional wavespeed structure of the Earth by fitting seismic travel time data collected at surface stations. Data interpolation and denoising techniques are important pre-processing steps that use prior knowledge about the data, including parsimony in the frequency and wavelet domains, low-rank structure of matricizations, and local smoothness. We show how local smoothness structure can be combined with low rank constraints using level-set optimization formulations, and develop a new relaxation algorithm that can efficiently solve these joint problems. In the seismology setting, we use the approach to interpolate missing stations and de-noise observed stations. The new approach is competitive with alternative algorithms, and offers new functionality to interpolate observed data using both smoothness and low rank structure in the presence of data fitting constraints.

Here are some of the fitting results with our algorithm, and some other competing methods.

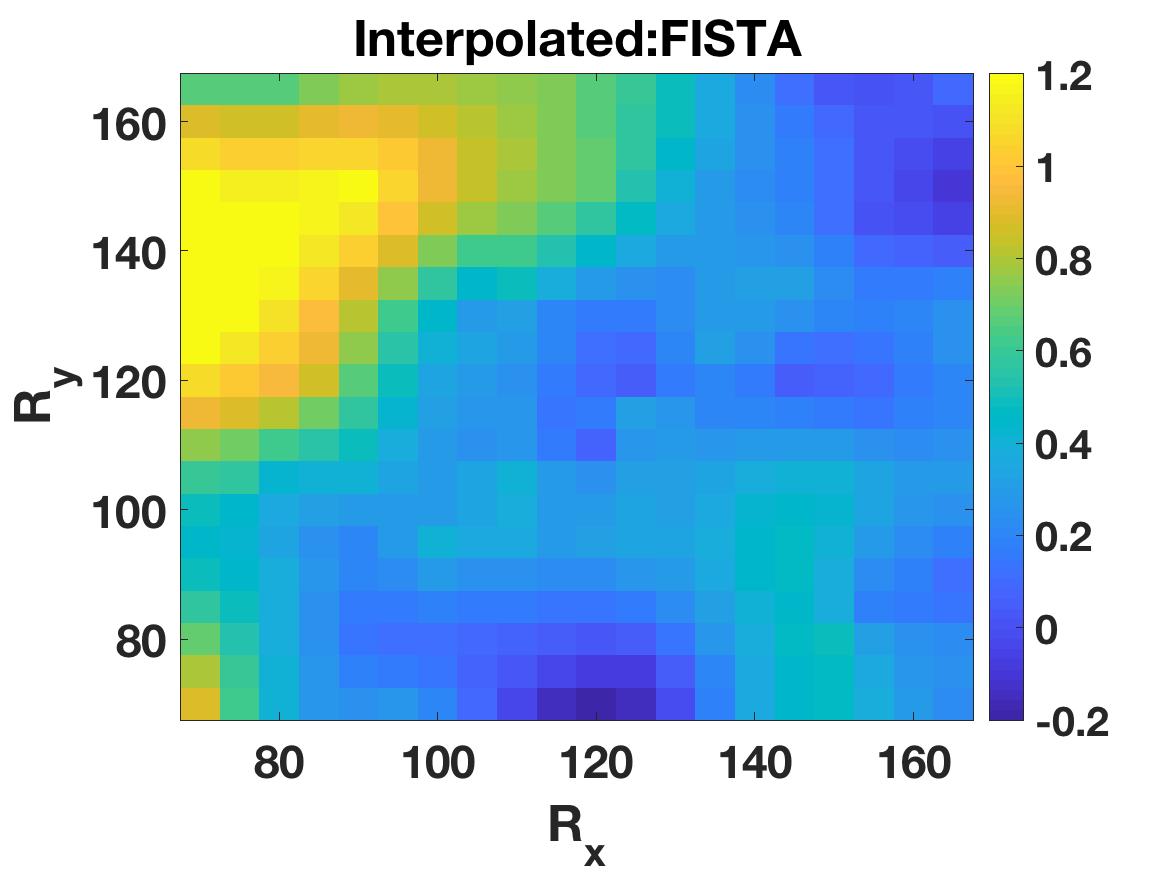
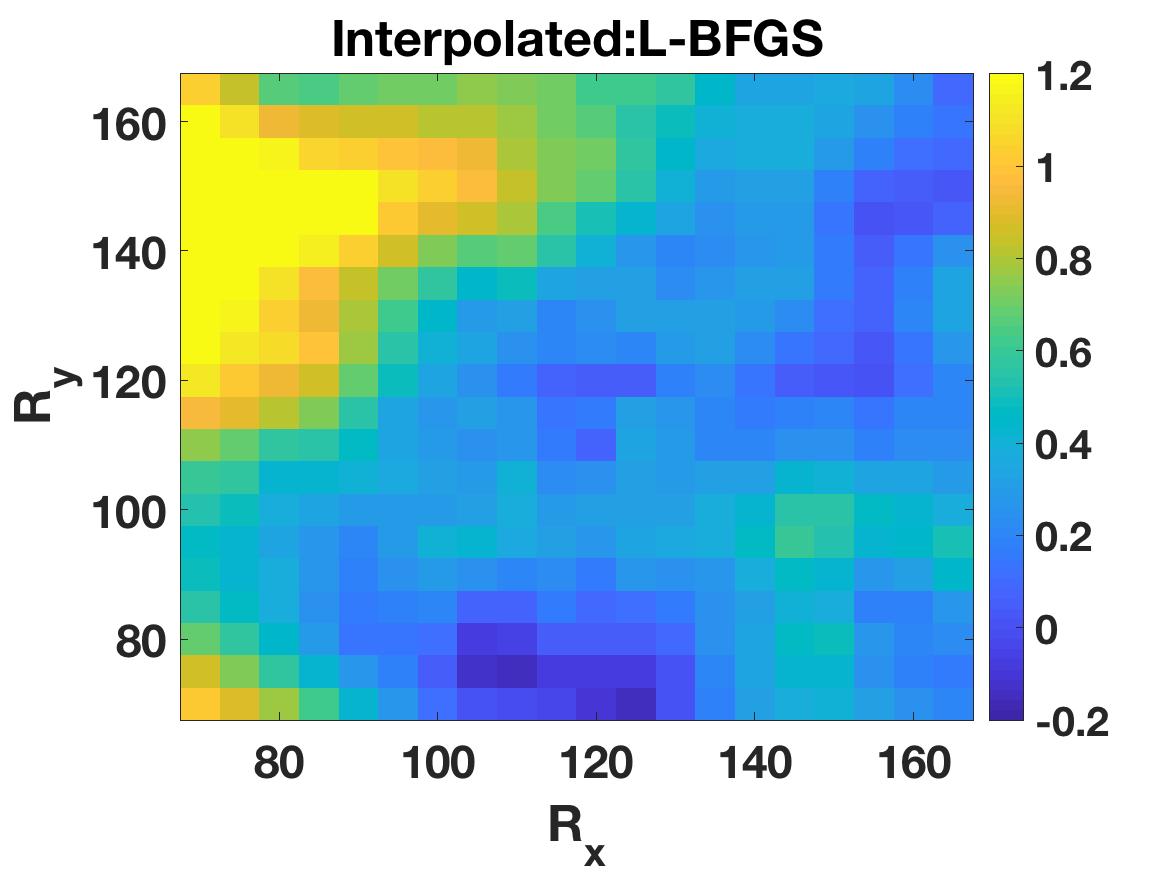
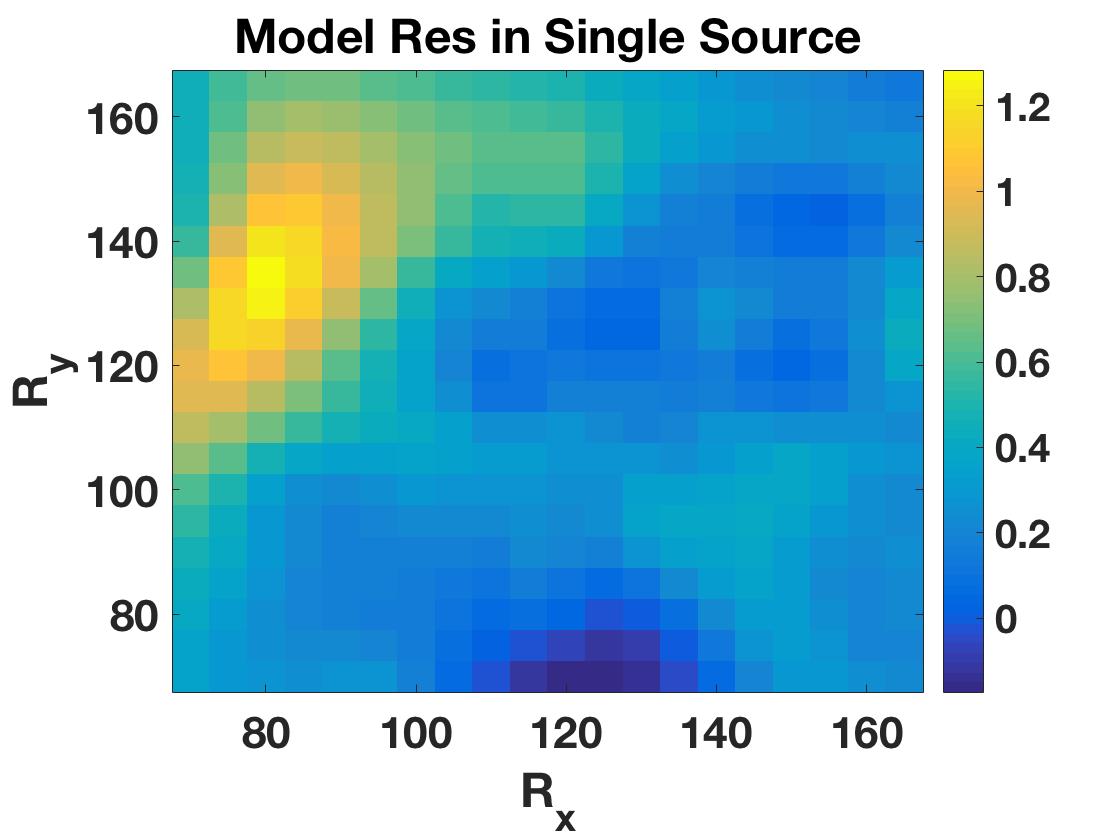
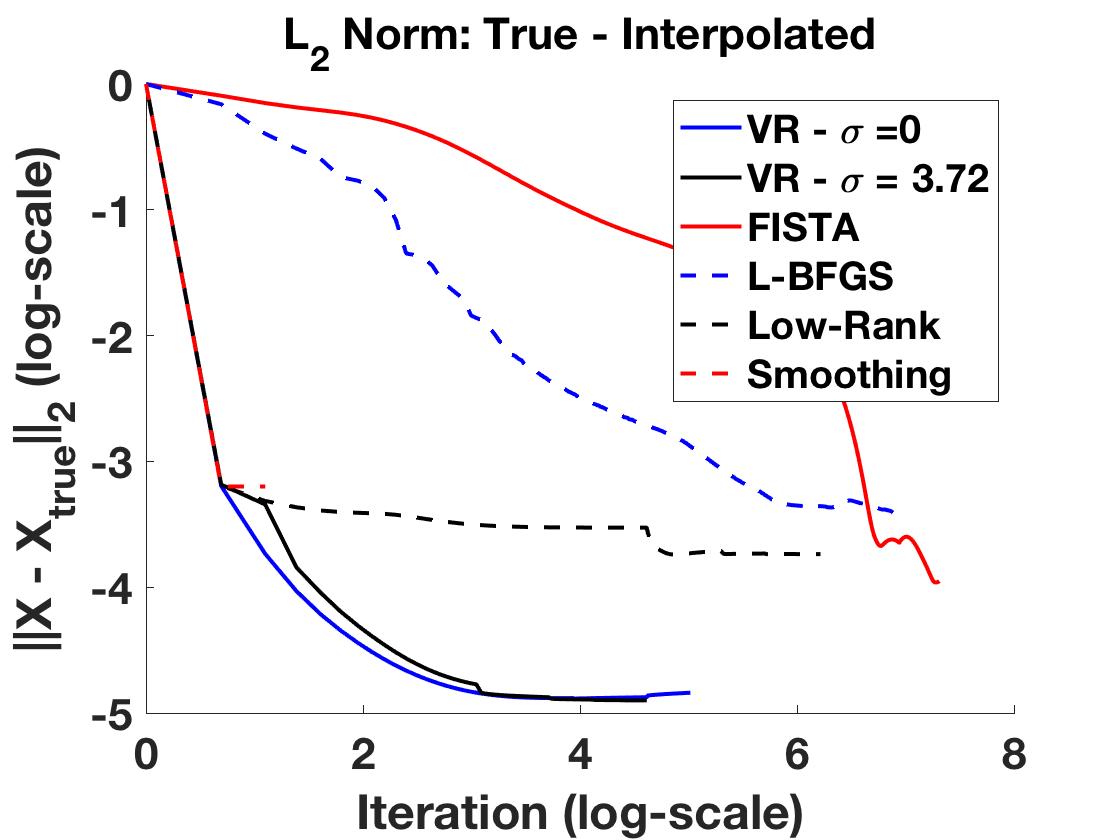
Poster presentation from the DOE CSGF Annual Conference in Arlington, Virginia