Basis Pursuit Denoise with Nonsmooth Constraints
This was a project that we (Sasha and I) developed while working with Rajiv Kumar on an extension of a previous method (SR3 relaxation) and project (with curvelets that failed to become anything). It was accepted by IEEE Transactions on Signal Processing, and a copy can be found here. I presented a poster at the DOE program review in July of 2019.
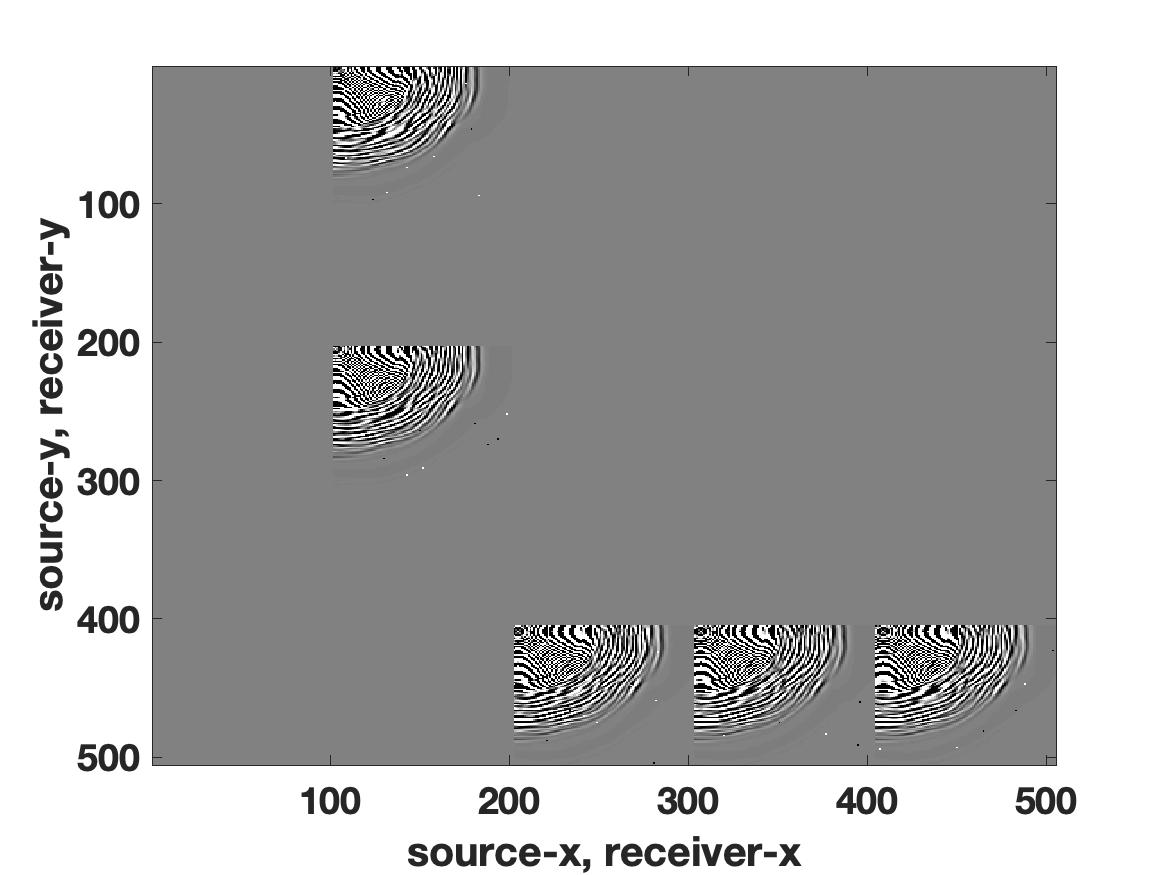
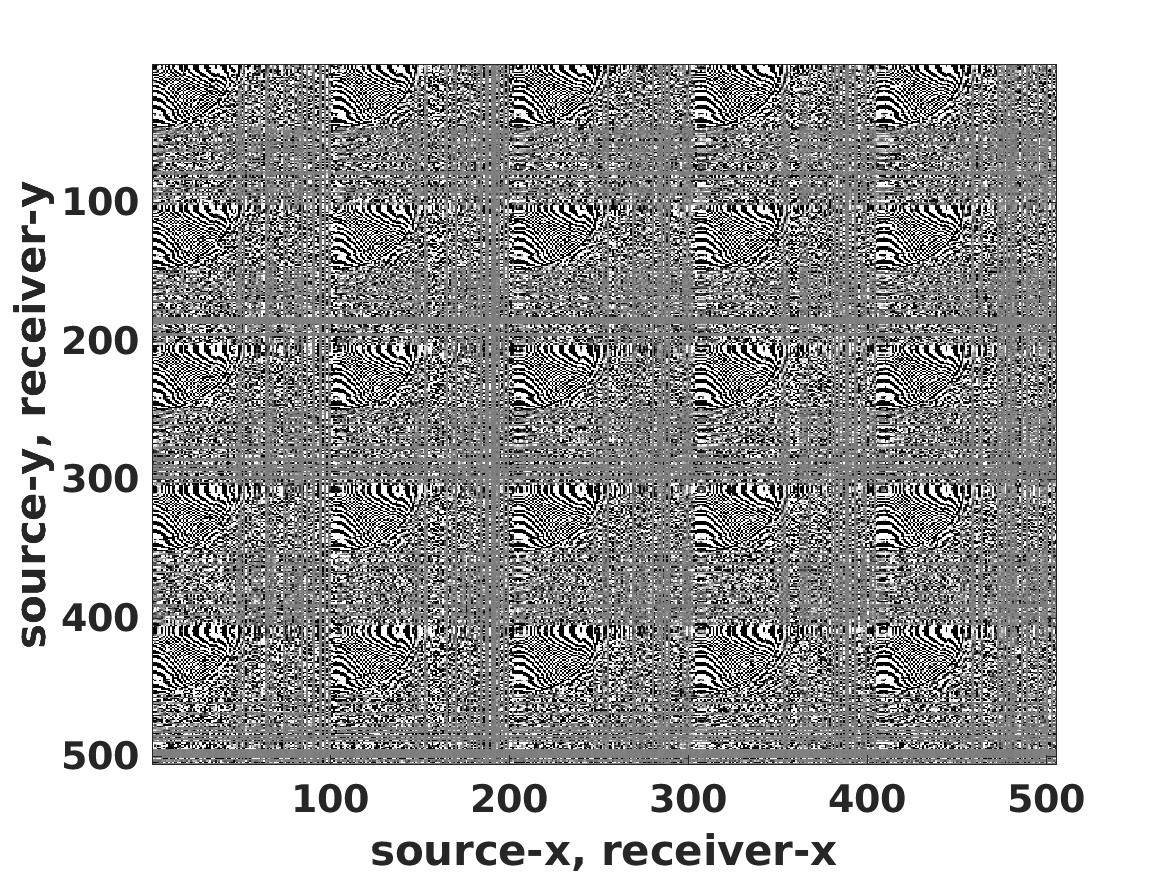
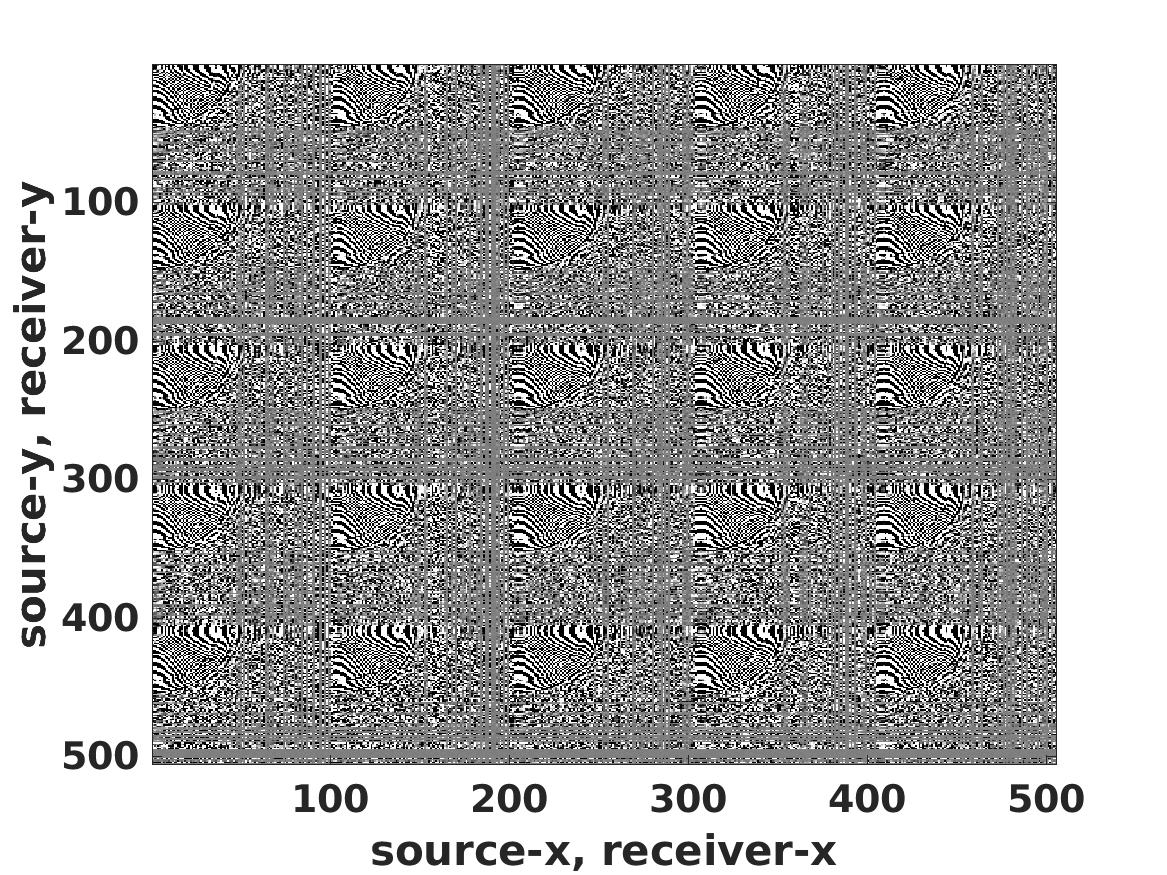
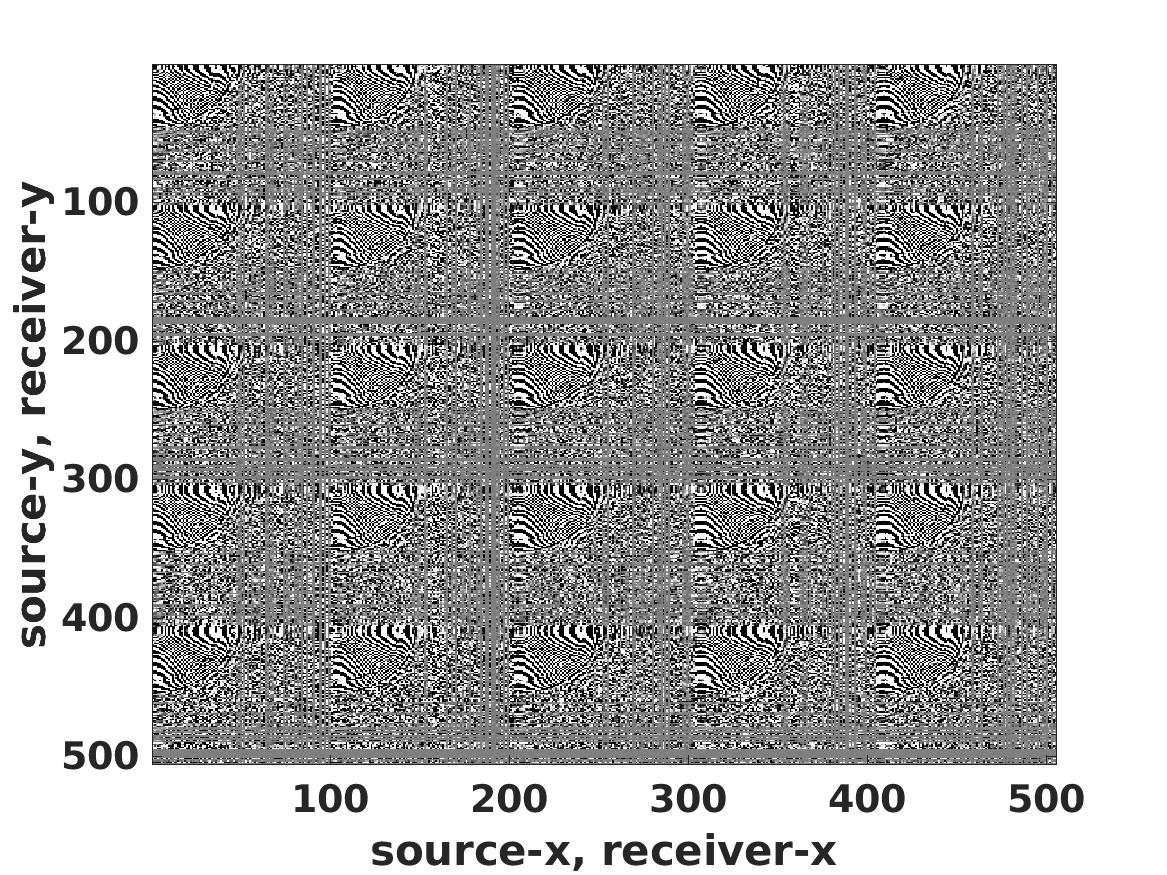
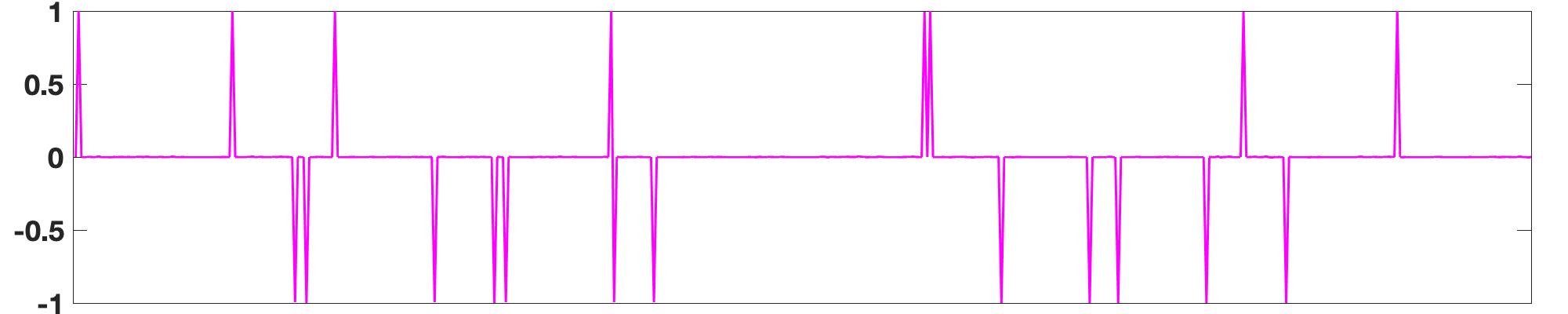
Level-set optimization formulations with data-driven constraints minimize a regularization functional subject to matching observations to a given error level. These formulations are widely used, particularly for matrix completion and sparsity promotion in data interpolation and denoising. The misfit level is typically measured in the l2 norm, or other smooth metrics. In this paper, we present a new flexible algorithmic framework that targets nonsmooth level-set constraints, including L1, Linf, and even L0 norms. These constraints give greater flexibility for modeling deviations in observation and denoising, and have significant impact on the solution. Measuring error in the L1 and L0 norms makes the result more robust to large outliers, while matching many observations exactly. We demonstrate the approach for basis pursuit denoise (BPDN) problems as well as for extensions of BPDN to matrix factorization, with applications to interpolation and denoising of 5D seismic data. The new methods are particularly promising for seismic applications, where the amplitude in the data varies significantly, and measurement noise in low-amplitude regions can wreak havoc for standard Gaussian error models.